Research Projects

Since the strength of the Stokes varies within the wave group, there is a divergence in the mass transport. This pushes water down in the front of the group, and brings it up in the rear, creating a deep return flow. This flow can then wiggle the isopycnals of the underlying stratification, thereby making internal gravity waves. It turns out that this flux of energy from surface to internal waves is too weak to be relevant for the surface waves (the group would travel multiple times around the Earth before losing half it's amplitude!), but this may help explain the observed spectral peak in high frequency internal waves. This work is in collaboration with Prof. William Young, and has been submitted to the Journal of Fluid Mechanics (pdf). I recently gave a talk on this work at the International Symposium for Stratified Flows (pdf).

Submesoscale instabilities in the Bay of Bengal

The Bay of Bengal receives a tremendous amount of fresh water input from rivers in the north. These fresh waters butt up against saltier waters of the Indian Ocean creating very strong horizontal density gradients that are salt stratified. The mixed layers in and around these fronts can be as shallow as a several meters. I am currently using a linear stability code that I developed during my Ph.D.(see chapter 3 of my thesis) to analyze these frontal regions. This work is in colloaboration with Prof. Jennifer MacKinnon and is still in the early stages, but here is some of the latest great work that has been done on the Air-Sea Interactions in the Northern Indian Ocean - Regional Initiative (ASIRI) project.

Surface wave modified submesoscale instabilities

The Stokes drift associated with surface waves results in a Stokes Coriolis force, and a Stokes sheer force that may modify the mean and turbulent flows in the ocean mixed layer.For a flow in Lagrangian (Eulerian + Stokes) thermal wind balance, several mixed layer instabilities may arize including baroclinic and symmetric instabilities. Here is a video of symmetric instabilities in the absence of Stokes drift.

Stokes drift changes the vertical shear, and therefore the Richardson number in the upper part of the layer, so one might expect that Stokes drift affects onset or strength of symmetric instabilities. It turns out that, regardless of the Richardson number, symmetric instabilities arise when the potential vorticity (PV) takes the opposite sign to the Coriolis frequency, f. The movie below on the left shows the PV evolution in two fronts with Stokes drift. Symmetric instabilities develop in regions of very negative PV, and deposit negative PV into the pycnocline, and lift positive PV into the mixed layer. The movie below on the right shows the perturbation cross front velocity. Once symmetric instability develops you can see the cannonical banded structures that are parallel to isopycnals similar to the previous video without Stokes drift.

Stokes drift also modifies baroclinic instabilities, but only slightly. To read more on this, see the published paper here (pdf) (doi), or the talk I gave in 2015 (pdf).

Stokes Drift and Shear Instabilities in Fronts

Stokes drift is often associated with instabilities that form Langmuir turbulence. These Langmuir instabilities draw energy from the Stokes shear, and from the Eulerian shear. In the previous section we saw that Symmetric instabilities draw energy from the Eulerian shear, but not from the Stokes shear. Holm (1996) showed analytically that a Lagrangian mean Richardson number (i.e. a Richardson number using the Lagrnagian mean shear) less than 0.25, is sufficient for Kelvin-Helmholtz instabilities. In addition, Holm showed that an inflection point in the Eulerian velocity is necessary for Kelvin-Helmholtz instabilities. We confirm these criteria with nonlinear, large eddy simulations. Kelvin-Helmholtz rolls can be seen in the video of the buoyancy evolution below.

Since Langmuir turbulence draws energy from both the Eulerian shear and Stokes shear, the additional of geostrophic (Eulerian) shear in a front can fuel the instability. However in practice, the geostrophic shear is far weaker than the Stokes, and ageostrophic Eulerian shears. Therefore, the primary effect of a front on Langmuir turbulence is to suppress it when the front slumps and vertical stratification is increased (or enhance turbulence if the front is steepened).

For more on this subject, see a talk I gave at the Ocean Science Meeting in 2016 (pdf).

Hurricane Wake Restratification

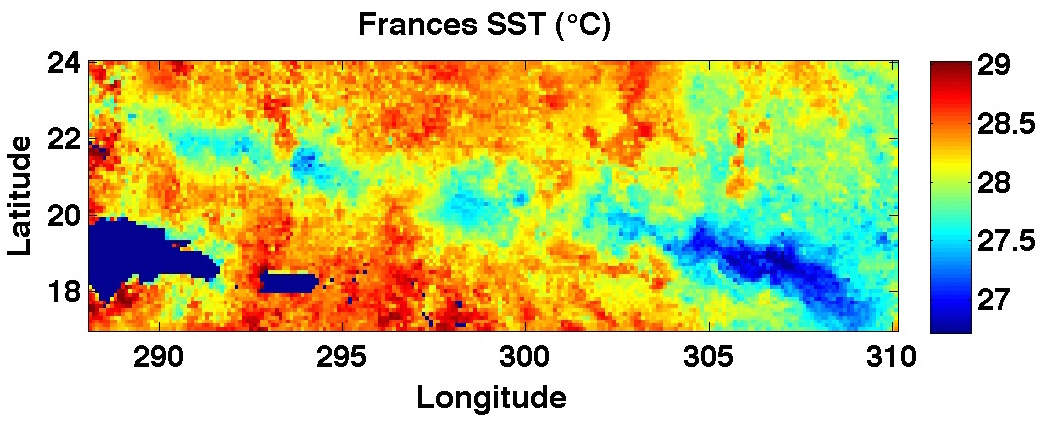
When a hurricane passes over the ocean, intense winds mix the upper ocean mixed layer with the uncerlying water in the thermocline, resulting in a cooler surface temperature, and less stratified (than befor the storm) layer of water. This is referred to as the hurricane wake. The image above shows the cold wake of hurricane Frances in the Atlantic in 2004. For reference, in the bottom left corner are the islands of Hispanola and Puerto Rico. Recently, the NASA Observatory highlighted a nice image of the wake from Hurricane Nicole in October 2016.

The timescale and mechanism for hurricane restratification can have implications for the local ecology, future sea surface temperature conditions that might affect future hurricanes, and the meridional heat transport. The restratification of hurricane wakes has been considered in the past as a one-dimensional process where the surface heat flux simply warms the wake. However, since a very strong wake makes very strong horizonal density fronts along the sides of the wake, two-dimensional (Ekman buoyancy fluxes) and three-dimensional (mixed layer eddies) processes may play a role in the restratification. For deep, narrow wakes mixed layer eddies and Ekman buoyancy fluxes restratify the wake as fast as solar restratification.

This work comprised a significant portion of my PhD, and was in collaboration with is Prof. Baylor Fox-Kemper. To read more on this topic, see our published paper here (pdf) (doi), or this short talk I gave in 2012 (pdf).